Free Access
Table I
Parameter values for the main scenario A and the alternative scenarios. Scenario B values were the same as for scenario A except that the number of parents per grandparent was 3 and annual budget per grandparent was 20.
| Parameters | Main scenario | Alternative scenarios |
|---|---|---|
Additive variance (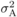 )a )a |
1 | 1 |
Dominance variance in proportion of the additive variance
(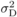 )b )b |
0.25 | 0; 1 |
Narrow-sense heritability (h2)
(obtained by changing  )c )c |
0.125 | 0.05; 0.2; 0.5; 1 |
| Coefficient of additive variation at mature age adjusted by the correlation between observed value | 11 | 5; 15 |
| and value for forestry, % (CVAm)c | ||
| Number of grandparents (Ngandparents)c | 50 | 50 |
| Number of parents mated within each family and expressed per grandparent (p) | 6 | To be optimised |
| Weight for group coancestry | 0 | 100 |
| Breeding population size (NBP) | 300 | (= 50p) |
| Time not used for testing, years (Tnot − testing)c | 5 (top-grafts) | 4; 10 (grafts) |
| Testing time, years (Ttesting)c | 15 | To be optimised |
| The fixed costs per grandparent, “plants”(Cfixed)c | 100 | 0; 200 |
| Cost of one parent, “plants”(Cparent)c | 50 | 0; 100 |
| Cost of one test plant, “plants”(Cplant)c | 1 | 1 |
| Annual budget per grandparent, “plants”(the constraint)c | 50 | 30; 40; 70; 100 |
| Annual genetic gain (or group merit), % | To be maximized | |
a
The additive variance in the observed values used for selection. It is convenient to set the additive variance as 1 and to express the other variance components as proportions of the additive variance.
b
The dominance variance makes up 25% of additive variance in a forest tree breeding population and is a rather typical value used in similar studies (e.g. Danusevičius and Lindgren, 2002).


