| Issue |
Ann. For. Sci.
Volume 67, Number 4, June 2010
|
|
|---|---|---|
| Article Number | 404 | |
| Number of page(s) | 9 | |
| DOI | https://doi.org/10.1051/forest/2009124 | |
| Published online | 02 April 2010 | |
Original article
Efficiency of breeding strategy where grandparents – but not parents – contribute equally to the breeding population
Efficacité de la stratégie de sélection où les grands-parents – mais pas les parents – contribuent également à l’amélioration de la population
1
Lithuanian Forest Research Institute, Liepu 1, Girionys, 53101, Kaunas
district, Lithuania
2
Faculty of Forest and Ecology, Lithuanian Agricultural University, Studentu
11, 53361 Akademija, Kaunas district, Lithuania
3
Department of Forest Genetics and Plant Physiology Swedish University of
Agricultural Sciences
901 83
Umeå, Sweden
* Corresponding author:
d.danusevicius@mi.lt
Received:
12
May
2009
Accepted:
8
October
2009
• The objective was to optimise the strategy for maintaining the genetic balance in long-term breeding where the grandparents contribute equally to the breeding population, but the parents do not.
• The annual genetic progress under a budget constraint was compared for a number of scenarios. The factors considered were: genetic parameters, recruitment population size, mating number per grandparent, cost of plants and parents, selection age and time components. Phenotypic selection forward was assumed. Using more parents than grandparents affects the testing population only, thus, gene diversity loss and breeding population size remain constant.
• Using larger number of parents than grandparents was a superior strategy at all scenarios tested. The strategy with 6 parents per grandparent and 1% of the tested plants selected on their phenotype at age 15 for further mating is recommendable. The strategy to choose 6 parents per grandparent was robust over a heritability range 0.05 to 0.2. At a higher heritability, the optimum number of parents per grandparent was 2 to 4.
• Using larger number of parents than grandparents has the potential to improve annual genetic gain in the magnitude of 50% compared to the strategies currently used for Scots pine in Sweden.
Résumé
• L’objectif était d’optimiser la stratégie pour le maintien de l’équilibre génétique dans une sélection à long terme où les grands-parents, mais pas les parents, contribuent également à l’amélioration de la population.
• Le progrès génétique annuel sous une contrainte budgétaire a été comparé pour un certain nombre de scénarios. Les facteurs considérés sont les suivants: les paramètres génétiques, la taille de la population de recrutement, le nombre de croisements par grand-parent, le coût des plants et des parents, l’âge de sélection et les composantes temporelles. La sélection phénotypique précoce a été prise en charge. Utiliser plus de parents que de grands-parents a seulement un effet sur la population d’essai, donc, la perte de la diversité génétique et la taille de la population améliorée restent constantes.
• L’utilisation d’un plus grand nombre de parents que de grands-parents est une stratégie supérieure pour tous les scénarios testés. La stratégie avec 6 parents par grands-parents et par 1 % des plants testés sur leur phénotype à l’âge de 15 ans par croisement supplémentaire est recommandable. La stratégie du choix de 6 parents par grand-parent a été robuste sur une échelle d’héritabilité de 0,05 à 0,2. Lors d’une héritabilité plus élevée, le nombre optimal de parents par grand-parent était de 2 à 4.
• L’utilisation d’un plus grand nombre de parents que de grands-parents a le potentiel d’améliorer le gain génétique annuel de l’ordre de 50 % par rapport aux stratégies utilisées actuellement pour le pin sylvestre en Suède.
Key words: balanced selection / long-term breeding / gene diversity / optimising / Pinus sylvestris
Mots clés : sélection équilibrée / sélection à long terme / diversité génétique / optimisation / Pinus sylvestris
© INRA, EDP Sciences, 2010
1. INTRODUCTION
The response to selection in a population with a family structure can be maximised by combined index selection or by more sophisticated indices assigning a value to the relatives (Falconer and McKey, 1996). However, much weight on family values will often lead to an unacceptably low gene diversity and a high degree of relatedness, at least when applied to forest tree breeding (e.g. Wei, 1995). Long-term breeding requires efforts to maintain gene diversity in the breeding stock. This can be achieved by making the parental genetic contributions similar and in its extreme case it could be visualised as within-family selection. Swedish conifer breeding has basically applied a strategy of an equal parent contribution to the breeding population and in multi-generation simulations it turned out to be a sustainable strategy not much improved by a higher representation of the better parents (Rosvall, 1999). Equal parental contributions are made at the cost of genetic gain, what calls for improvements of these strategies to maximise the genetic gain per unit of the gene diversity lost (Lindgren, 2005).
“Balanced selection”is used in the meaning that ancestors contribute equally to the following generation of the breeding population, e.g. Sanchez (2000) used it in this meaning but restricted the balance to the parents. The specific circumstance our study is focusing on is that the parental contributions to the next generation testing (candidate) population are variable, but the grandparent contributions are balanced.
Kerr et al. (1998) introduced methods for considering the relatedness of the candidates used in animal breeding into forest tree breeding. The strategies were compared for gain over a number of generations with a testing population of 6000 trees per generation where selection was mainly on breeding values obtained by proper weighting of phenotype and relatives. Parents, matings and generation shifts were assumed free in terms of resources, but there was a penalty on the genetic gain for the increase in inbreeding similar to the penalty of group coancestry used by Lindgren and Mullin (1997). The number of parents, their contributions, their mates and the progeny size are generated by algorithms and generally not predefined.
In Swedish Scots pine breeding program the diversity is maintained mainly by keeping the breeding population size at 50 in a balanced mating and selection design (Hannrup et al., 2007; Rosvall, 1999) so each parent contributes two offspring to the next generation. An unbalance was allowed at the initiation of breeding only, when the founders with high breeding value were allowed to contribute to the future breeding (Ruotsalainen, 2002).
As regards the benefit per unit of time, clonal testing appears as the most efficient long-term cycling strategy, but when the cloning is not possible as for Scots pine, a two-stage cycling strategy of phenotypic pre-selection followed by progeny testing seemed advantageous (Danusevičius and Lindgren, 2002). A cycling strategy based on phenotypic selection has its advantages. It is simple and fast. It is preferable to a progeny-test strategy if heritability is high or budget is low (Danusevičius and Lindgren, 2002; Hannrup et al., 2007).
There is at least one alternative to keep the loss of gene diversity per generation at the same level while benefiting from a less balanced selection among families, and that is to use a larger testing population to compensate for a higher degree of unbalance among the parents, but keep the grandparental contributions equal (Lindgren et al., 2008). This strategy turned out to have a large potential to generate genetic gain per breeding cycle. However, to efficiently utilise this potential, optimisation of common long-term breeding scenarios as well as information about its limits and robustness are needed.
Relations with grandparents are familiar and easily visualized and understood. For most breeding programs, which have passed their infancy, the initial selections are either parents or grandparents to the testing population, thus there is a little need to go longer back in the ancestry. Grandparents can be reasonably well recorded; to go longer back in the ancestry is often administratively, pedagogically and by conception difficult. For numeric and administrative computing and analyses, it is probably sufficient to go back to grandparents to get acceptable accuracy. If relating to founders instead of grandparents, it could be difficult to quantitatively define the differences in unbalance in a practical way in advanced generations.
The objective of this study was to investigate efficiency of the strategy with relaxed parental but balanced grandparental contribution to a range of circumstances relevant for practical forest tree breeding with special reference to Scots pine in central Sweden.
2. MATERIALS AND METHODS
2.1. The grandparent-balance strategy
The Swedish Scots pine breeding program was chosen as a case of long-term breeding strategy (described by Hannrup et al., 2007). The traditional parent-balance strategy is here represented by cycles with single-pair mating (SPM) and balanced within-family selection forward of the two best phenotypes within each family as parents for the next cycle matings (Fig. 1 left). We used SPM for convenience of calculation and mating type is not a basic feature of the strategy. To facilitate the interpretation of the results between the SMP and other mating strategies, we expressed the number of parents per grandparent instead of per family (to obtain number of parents selected within each family PGP is multiplied by 2 with SPM).
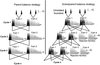 |
Figure 1 Two balanced breeding strategies are compared. A sub-line initiated by four founders is shown. The connected lines show the pairs mated. To the left “parent-balance”strategy with within-family selection only, where two families are created and after testing the two best individuals in each are mated. To the right “grandparent-balance”strategy with both within- and among-family selection, where four but smaller families are created and after testing the best two individuals in each of the two best families are mated. |
The suggested improvement of the above given “parent-balance”strategy is the “grandparent-balance”strategy where the new idea is to mate more than two parents from each family and so generate additional genetic gain (Fig. 1 right). The balance is maintained so that the grandparents have equal representation in the breeding population at a certain time, but the parents need not be equally represented in the breeding population even if they become equally represented in retro-respect when they become the grandparents.
The breeding population size of the grandparent-balance strategy is the same as of the parent-balance strategy (Fig. 1), however, if the balance is kept among the grandparents instead of parents, more families can be created and tested in the parental generation. The improved strategy can be considered as a type of combined selection, where the phenotype of an individual is considered for selection but also information about the family and its parents is available. However, to simplify calculations, the selection is done in tandem, first families and then individuals within family.
2.2. The model
A complete breeding cycle from the crosses to the selection of the parents for the next cycle of crosses was followed. G × E interaction, change of heritability over generations and epistasis were not considered. Mean breeding value of the grandparents was set to zero. An infinitesimal genetic model was assumed.
Annual group merit (see below) was maximized – for most scenarios that is equivalent to maximizing annual genetic gain at a budget constraint per year and grandparent. At each testing time, the optimization was carried out by varying the number of parents per grandparent and the family size to fit into the budget. With the fixed annual budget, the optimisation searched for an optimum balance between testing fewer but larger families and getting more gain from “within family selection”or testing more but smaller families and getting an additional gain from “among family selection”. More details about the concepts and mathematical framework are given on the web and by Lindgren et al. (2008).
The selections are made for a selection index based on observed traits resulting in gain in the target trait (assumed the value for forestry at mature age). To get quantitative gain estimates a reduction is needed to consider uncertainties in “value for forestry”. The criterion of genetic progress is group merit (Danusevičius and Lindgren, 2002), which is genetic gain with diversity loss subtracted (Wei and Lindgren, 2001). For most calculations in this study the value of the diversity loss was set to zero and then the annual progress in group merit became annual progress in genetic gain. The loss of gene diversity per breeding cycle was kept constant at the grandparent-balance strategy. However, the cycling time may vary and, thus, annual gene diversity loss may vary.
Parameter values for the main scenario A and the alternative scenarios. Scenario B values were the same as for scenario A except that the number of parents per grandparent was 3 and annual budget per grandparent was 20.
The annual progress in Group Merit
(GMannual, equal to annual gain for most
cases as c = 0) was calculated. The gain over a breeding cycle is the sum
of the response to among and within family selection: 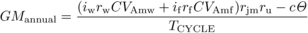 (1)where the indices w and f indicate within and among
family selection, iw and if are
among and within family selection intensity (predicted selection response in standard
deviation units); rjm is juvenile-mature genetic correlation
between the observed trait and the “target trait”; CVAmw and
CVAmf are coefficients of variation in
breeding value for the “target trait”at mature age for within and among family selection;
ru is correlation between the “target trait”and the “real
value for forestry”as explained in Scenarios sub-section;
c the weight factor for the loss of gene diversity that converts the
genetic gain and diversity to the same scale; Θ is loss of gene diversity
per breeding cycle. For this study Θ = 0.01 (=0.5/50 considering that a
Swedish compartment of the breeding population comprises 50 founders, Hannrup et al.,
2007); TCYCLE is
breeding cycle time in years; rf and
rw is correlation between true and predicted breeding values
calculated for among and within family selection. The expressions in formula (1) are
developed:
(1)where the indices w and f indicate within and among
family selection, iw and if are
among and within family selection intensity (predicted selection response in standard
deviation units); rjm is juvenile-mature genetic correlation
between the observed trait and the “target trait”; CVAmw and
CVAmf are coefficients of variation in
breeding value for the “target trait”at mature age for within and among family selection;
ru is correlation between the “target trait”and the “real
value for forestry”as explained in Scenarios sub-section;
c the weight factor for the loss of gene diversity that converts the
genetic gain and diversity to the same scale; Θ is loss of gene diversity
per breeding cycle. For this study Θ = 0.01 (=0.5/50 considering that a
Swedish compartment of the breeding population comprises 50 founders, Hannrup et al.,
2007); TCYCLE is
breeding cycle time in years; rf and
rw is correlation between true and predicted breeding values
calculated for among and within family selection. The expressions in formula (1) are
developed: 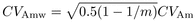 (2)
(2)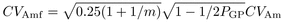 (3)
(3)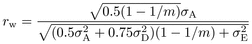 (4)
(4)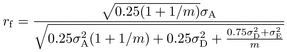 (5)where
(5)where 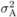 is additive variance,
is additive variance,
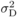 is dominance
variance;
is dominance
variance; 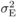 is environmental
variance (for observed traits, values in Tab. I);
PGP is number of candidate parents selected per grandparent;
m is offspring family size.
is environmental
variance (for observed traits, values in Tab. I);
PGP is number of candidate parents selected per grandparent;
m is offspring family size.
Scenario A. Considerations of number of parents per grandparent (PGP). This table is for variants of the main scenario where annual cost per grandparent is 50 and PGP is variable. PF is the proportion of plants selected as parents for the breeding population.
Scenario B. Considerations of parents per grandparent (PGP). Here the gain is given in percentage of that maximizing gain per year for different deviations from the optimal testing. “n.p.”means “value not possible”. PF is the proportion of plants selected as parents for the breeding population.
The additive genetic variance was adjusted due to the limited numbers available for selection. Within a full sib family (Eq. (4)), the additive variance is half and the dominance variance 3/4 of the total. The variance among the family means is reduced in a small family. Additive variance among full sib families (Eq. (5)) is half of that in a population for unrelated families but one quarter for cousin families, which share grandparents. If parents come from the same full sib family the variance in additive value among them is half of what it is if parents come from unrelated full sibs. Small families widen the among-family variation (Eq. (4)), but few selection options (candidate parents) reduce the variance.
The optimisations were run with a fixed total cost
(Ctotal)expressed per breeding cycle and grandparent with
“test plants”as the cost units (one tested plant is one cost unit) as follows:
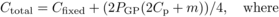 (6)Cfixed is fixed cost per
grandparent for the costs which are little dependent on the number of parents mated per
grandparent: the costs of establishment, maintenance (including fencing) and measurements
of the field trials and the costs of the data analyses; Cp is
cost of parents to be mated were assumed to include costs of collecting of scions and
grafting them for further recombination and the costs of forming the new generation
(mating and the related activities); m is offspring family size. The term
(2Cp + m) expresses the cost of one family
(Cp is multiplied by 2, because 2 parents are used to create
one family with SPM); PGP is the number of candidate parents
selected per grandparent.
(6)Cfixed is fixed cost per
grandparent for the costs which are little dependent on the number of parents mated per
grandparent: the costs of establishment, maintenance (including fencing) and measurements
of the field trials and the costs of the data analyses; Cp is
cost of parents to be mated were assumed to include costs of collecting of scions and
grafting them for further recombination and the costs of forming the new generation
(mating and the related activities); m is offspring family size. The term
(2Cp + m) expresses the cost of one family
(Cp is multiplied by 2, because 2 parents are used to create
one family with SPM); PGP is the number of candidate parents
selected per grandparent.
An EXCEL-based deterministic simulator “Breeding Cycle Analyser Wilhelm”sheet was used for this study. The sheet with more detailed explanations can be found at www.mi.lt/research.htm or http://wwwgenfys.slu.se/staff/dagl/Breed_Home_Page/
Testing time considerations. The testing time of 15 y was chosen for the main scenario. Here the annual group merit at some testing times is presented as percentage of the test time maximizing group merit per year for different deviations from the optimal testing. Annual gain and annual group merit are identical unless group coancestry gets a weight, which it does not in the main scenario. While testing an alterative parameter value, the other values are kept at the main scenario values (number of parents per grandparent is 6 (12 per family with SPM)).
 |
Figure 2 Optimal number of parents per grandparent as a function of annual budget (a). Annual gain as a function of the number of parents per grandparent (b). Three curves are shown for different costs per parent (Cparent = 50 for main scenario). Optimum number of parents per grandparent for the main scenario annual budget (50) are indicated by dots on the curves. |
2.3. The scenarios
Two main scenarios A and B and a number of alterative scenarios were used in the optimization. Scenario A reflects the present-day foreseen values for Scots pine breeding in Sweden (Tab. I). Scenario B reflects a situation when the budget is lower than anticipated today (Tab. III). When an alternative value for any parameter was tested, all the other parameters were kept at the main scenario values. The inputs were chosen for their relevance to breeding of Scots pine in central Sweden. A most likely value was set as the main scenario value (Tab. I) and reasonable upper and lower limits for each value were selected (Hannrup et al., 2007; Rosvall, 1999; Rosvall et al., 2001).
The choice of a relevant juvenile-mature (J-M) correlation function and relevant parameters of that function was discussed by many authors (e.g. reviews in Danusevičius and Lindgren, 2004; Jansson et al., 2003). We used an average of the J-M functions in Jansson et al. (2003) for pooled data from progeny tests of Scots pine in southern Sweden. This function was close to the most used function by Lambeth(1980).
The coefficient of additive variance in the northerly Scots pine genetic tests averaged to 14% (Rosvall et al., 2001). To consider limited number of sites with different characteristics (“correction for G × E”), the value of CVAm was adjusted for the correlation between the “measured trait”and the “value for forestry”(ru) leading to ruCVAm value of 12.5%, it can also be seen as a reduction of CVAm to make it applicable on all sites (for Scots pine volume production at mature age, Rosvall et al., 2001). Results by Hannrup et al. (2007) may hint on a marginally lower value. There are more factors reducing ruCVAm, although quantitative estimates has rarely – if at all – been presented: (a) the testing sites do not represent actual future forest plantation sites and the tests are not managed as forests; (b) the environments change not only geographically, but also among years including long-term changes as global warming; (c) forest management and the value criteria change over time; (d) the accuracy of genetic entries are not symmetric as assumed in the formulas; (e) CV is based on the variation among the plus-tree progenies in tests, which include provenance variation, maternal effects, epistasis, “after-effects”, a variable amount of inbreeding and genetic disequilibrium; (f) CVAm is somewhat inflated in experiments as bad progenies become outcompeted by good. In our study, the effects of the above listed factors are considered by reducing ruCVAm to 11%.
The cost estimates (Tab. I) for the main scenario are derived based on Scots pine breeding in Southern Sweden (Almqvist 2009; Hannrup et al., 2007). The main scenario testing time was set to 15 y, which is close to optimum for a phenotype-based testing strategy (Danusevičius and Lindgren, 2002) and operationally suggested for Scots pine in central Sweden (Almquist, 2009).
3. RESULTS
3.1. Comparison between the parent- and grandparent-balance strategies
The annual genetic gain (and annual Group merit) differed with a factor larger than two among the reasonably assumed scenarios (Tabs. II to IV, Fig. 2b).
In none of the alternative scenarios the traditional parent-balance strategy (number of parents per grandparent PGP = 1) was superior to the grandparent-balance strategy with PGP > 1 (Tabs. II, III and Fig. 2b). For most scenarios, the genetic gain by the parent-balance strategy was in the magnitude of 65% of the grandparent-balance strategy with PGP at its optimum (Tabs. II and III). Only when the heritability was unrealistically high or the annual budget extremely poor, the parent-balance strategy was similar to the grand-parent balance, though it still was somewhat more efficient with PGP = 1.5 (Tabs. II and III).
3.2. Number of parents per grandparent and the share of the testing population used as parents
For the main scenario, the optimal number of parents per grandparent (PGP) was 6 (Fig. 2), which was used as a main scenario value. The optimal PGP varied much with the cost of the parent and the annual budget per grandparent (Tab. II, Fig. 2). The optimal PGP rose almost linearly with the increasing budget (Fig. 2a). The optimal PGP became flatter with cheaper parents (Fig. 2b).
For the main scenario A, PGP of 6 was a robust optimum, as it gave at least 95% of the gain at the optimal PGP value for all alternative scenarios, except when the heritability was high (≥ 0.5) (which is not realistic) or when the annual budget is low (< 30) (Tab. II). For the low-budget scenario B, PGP of 3 was more sensitive to the cost parameters and under the main scenario values a non-optimality of more than 5% was obtained if the economical factors (fixed total cost or parent cost) deviated reasonably from the standard assumptions (Tab. III). Thus, the choice of PGP seemed more important when the budget was tight.
For the main scenario A, the proportion of the plants selected as parents in the testing population (PF) was mainly dependent on the annual budget and was little dependent neither on the parental cost nor on the heritability (when reasonable low) (Tabs. II and III). To select 1 percent of the experimental plants as the parents seems a useful rule of thumb for all the realistic scenarios, with exception of those where the budget is the lowest. The proportion of the plants selected as parents becomes low if the heritability is unusually high and it can be high if the budget is low (Tab. III). It decreases slightly with increasing budget at high budgets, but at low budgets it seems to increase fast when the budget is decreased (Tab. III). The Swedish breeding plan using the phenotypic selection strategy roughly aims at selecting 50 from 10 000 individuals, thus, around 0.5%, which seems reasonable close, but still suggests that a somewhat larger breeding population may be motivated.
3.3. Testing time
The time for the measurements for the selection in field trials was 15 y in the main scenario A. Variations within a reasonable range in the weight for group coancestry, the rotation time or the cycle time not used for testing did not make the testing time of 15 y non optimal: maximum 2% of the annual genetic gain were lost compared to the optimal testing time of 15 y (Tab. IV). Neither did another selection age in the interval 12–18 y cause more than 5% loss of the gain compared to what was optimal within the model for all the parameters varied. (Tab. IV).
4. DISCUSSION
4.1. Annual progress in breeding value
This study demonstrates that a marked gain in breeding efficiency can be obtained by applying balance among the grandparents instead of the parents at many situations in balanced forest tree breeding. The main scenario A results in an annual genetic gain below 0.3%, and no realistic scenario gives an annual genetic gain above 0.4% (Tab. II). These annual gains are lower than in the projections of the seed orchard gains in the future (e.g. Lindgren et al., 2008). The annual gain is not strongly dependent on the changes in the resources at the main scenario values (Tabs. II and III). Thus increasing the gain is not mainly a question of more resources. The genetic gain over the foreseen rotation time (70 y) was in the magnitude of 20% and the assumed coefficient of variation in the genetic values among the trees in a stand was 14%, a higher annual progress would mean that improved and non-improved trees do not overlap and a still higher annual gain would increase the risk for significant side-effects of breeding. As long as the bred and the non-bred material overlaps, no important surprises can be expected at a late stage. Such overlap exists at the current improvement rates and makes breeding safe, but faster improvement would make breeding less safe.
4.2. Relevance for breeding – earlier suggested strategies and other species
When the costs and the time components are included into the model, the phenotype-based testing strategy has the potential to be a major alternative for long-term breeding and is favored to progeny testing (Hannrup et al., 2007). We suggest an improved and optimized version of the phenotype-based testing with relaxed parental but restricted grandparental contributions, which increase its efficiency for 1/3. Danusevicius and Lindgren (2002) suggested phenotypic pre-selection followed by progeny testing and selection of the best individuals in each family based on their breeding values as a better alternative than either progeny testing or phenotypic selection. If compared with the phenotype-testing at a reasonable budget, the superiority of this two-stage testing method appeared to be in the magnitude 20% of the annual group merit progress, but when the penalty on the diversity loss at cycling may be regarded high, and more recent consideration by the authors make us suggest around 10% superiority is more applicable to the circumstances relevant to Scots pine breeding. Phenotypic pre-selection followed by progeny testing may still be improved by phenotypically pre-selecting individuals in the better segments of the breeding stock and top-grafting them, so that they are available for pollination. If suitable pollen parents can not be effectively selected, crosses can instead be made with poly-mixes which need not be among best general combiners as only the selection backwards among the pre-selected is intended. A further alternative may be to make polycross with the pollen mixes from the phenotypic selections, and later make forward selections in the polycross progenies with fathers to be identified by markers. The combined strategy with PGP = 6 and 1 percent of the tested plants selected on their phenotype for mating at age around 15 seems recommendable, and superior to the other breeding strategies earlier suggested for Scots pine at the budget assumed.
Focus on this study is Scots pine in Sweden, but as inputs are varied around a main scenario, approximate estimates for other species and situations can be made. For instance, Norway spruce can be bred so clonal testing is central, thus a “plant”corresponds to ten ramets of a clone. That means that the heritability will be much higher and the budget (expressed as plants) much lower, which will press the parents per grandparent close to one (Tab. II), the other influences are lower fixed cost, lower parent cost and shorter rotation time, but the influence of these factors seem less important. Thus “the conventional”way without an excess of parents per grandparent seems good enough for Norway spruce breeding based on the clonal tests.
4.3. Possible improvements of the grandparent-balance strategy
The grandparent-balance can easily be combined with positive assortative mating (Lstibùrek et al., 2004a, 2004b; Rosvall, 1999) or similar with stratified sublining (Ruotsalainen, 2002). The positive assortative mating increases the range of the genetic values so the genotypes used for mass multiplication in seed orchards become better, even if the average breeding stock is not improved.
The concept of the grandparent balance strategy can be widened in different ways combining it with unbalances in different ways. A strategy could allow unbalance among the grandparents, but keep the “effective size”of the grandparents constant. It can be widened to a strategy allowing unbalances among the grandparents but compensate by a larger breeding population with more representation of the better part of the breeding stock (Lindgren, 2005). This can be done by introducing unbalances and combining that by using more grandparents in the breeding stock to compensate for the unbalance. More crosses among the chosen parents can be made (the gain calculations in this study assumed SPM), but once parents are selected more crosses per parent may be claimed to be possible at a neglectable price (once the flowers and the pollen are there, some more pollinations may appear trivial). With more crosses per parent, the chance that the genes of a good parent are lost because it happens to be mated by a bad one is reduced. More crosses per parent would improve the accuracy of the estimated breeding value of that parent, and for use as the parents to the seed orchards, a reliable estimate of the breeding value may be requested besides that the estimated breeding value is high. Thus, several crosses per parent are more important for the assumed top ranking parents, which are more likely to be the candidates for the seed orchards. The calculations suggest to first select the families based on their performance and then the best phenotypes in the selected families, but higher gain can be obtained by selecting parents on a combined index weighting family values and individual families, the grandparent balance can still be maintained and actually the loss of gene diversity could be marginally reduced if more families were represented in the selection of the breeding population.
Unbalanced selection can probably be slightly superior to the balanced selection (Rosvall, 1999; Sanchez, 2000) and even if the balanced grandparent selection is used for ease and transparency of calculations in this paper, we suggest applying more unequal parent contributions than grandparent contributions rather than limiting the strategy to balanced grandparent or founder contributions.
4.4. Relevance for breeding – mating system and number of parents per grandparent
Probably the benefit of the grandparent-balance strategy will rise if more than one mating per parent is made. The added cost of having more full-sib families beyond the cost of parents and the test plants seem almost neglectable.
The annual budget and the cost of parents were the major factors to consider for the optimal share of the plants selected in the testing population for the breeding population (Tabs. II and III). PGP = 6 seems to be a good approximation for all the scenarios considered except for variation in the budget and parental costs. If the budget is increased, the optimum PGP increases approximately proportionally (Fig. 2a). High heritability favours less unbalance and small PGP, but with the heritability ranging from 0.05 to 0.2 (which seems most realistic for Scots pine breeding), PGP of 6 will be very close to optimum for the main scenario assumptions on the budget and the parent cost. The optimal share of the testing population selected for the breeding population was approximately one percent for all realistic scenarios, with exception of those where the budget was low.
For the strategy of initiating breeding program with access to many potential founders, Lindgren et al. (1997) found that the cost components were more critical than heritability, while this study indicates the opposite (cf. Tab. II). In this study the population is constrained by the number of the grandparents, while in the former study there was an infinite source of unrelated parents and grandparents, which makes it important how wide starting material can be afforded.
Kerr et al. (1998) used an option 2, which is rather compatible with our study (except that an unbalance was accepted): the reduction in group coancestry per generation was fixed to 0.017 and the number of the parents was 66–92, indicating a parents-per-grandparent ratio around 2.5, which is close to the value in scenario B in this study. The other options studied by Kerr et al. (1998) result either in what is regarded as too fast loss of group coancestry with a very limited advance in gain or unrealistically many parents and less gain than option 2. Thus, the results by Kerr et al. (1998) seem compatible with the findings of this study.
It may be worth to invest in techniques to reduce the costs for production of parents (grafting and mating): the optimum number of parents and the genetic gain become higher and it becomes less important to hit an optimum than in case of expensive parents, which may allow flexibility for variable situations (Fig. 2b).
4.5. Relevance for breeding – time for matings
By top-grafting the selected genotypes can be operationally available for artificial pollination. Flower stimulation can help in producing the sexual structures. Jansson et al. (2003) based on J-M correlations, estimated from 13 Scots pine progeny tests, and economical considerations concluded on optimum selection age of 10 to 15 y. A 15-years-old progeny trial of Scots pine should generate sufficiently mature Scots pine in central Sweden to serve as females in crossing within a few years after the grafting. Male flowering may need more mature trees to get pollen from the majority and be less easy to stimulate. Based on own and others observations (not documented here), male flowering is unlikely to occur in a major part of the trees at ages around 17 and it would probably not be practical to visit all experimental sites, thus selection intensity would be reduced. The time window for male strobili collection in the field trials with pollen mature enough for extraction but not yet released is very short, just a few days, and it is probably logistically difficult to arrange unless the field trial is conveniently localized. It seems possible to get pollen as well as female flowers from top grafts and it is probably more operationally realistic to plan for pollen collection in that way, although the option to collect in field trials can be kept in mind if grafting fails or budget increases. In this study it has been assumed that tree breeding is a synchronous activity when all actions happen at the same time with the breeding stock. Reality is different, in Sweden Scots pine breeding is structured in 24 differently targeted breeding populations. In those having F1 material in field tests (and thus soon mature for selection of what is called parents in this study) two third has not got all planned material out in field tests yet (Persson et al., 2008). Thus, different segments of the testing population are likely to be of different age and the crossings can be arranged so males are selected when the majority of the trees get pollen (probably at age 20–23). As a last escape if there are not enough pollen producing trees is to pollinate the receptive females with a pollen mix for progeny-testing instead, that strategy seems the second best alternative to the strategy analyzed in this study (Danusevičius and Lindgren, 2004).
5. CONCLUSIONS
The strategy of using several times more parents than grandparents has the potential of a substantial improvement compared to a balanced strategy with equal number of parents and grandparents. One percent of the plants in the recruitment population selected for the breeding population is a suitable number.
Acknowledgments
We gratefully acknowledge the Swedish Association for Forest Tree Breeding and Lithuanian Science and Study Fund for financial support. Swedish breeders are given big thanks for fruitful discussions as this study arose from our discussions.
References
- Almquist C., 2009, Alternative strategies for Scots pine breeding in Sweden. Document dated 2009-02-12. [Google Scholar]
- Danusevičius D., and Lindgren D., 2002. Comparison of phenotypic, clonal and progeny supported selection in long-term tree breeding. Silvae Genet. 51: 19–26. [Google Scholar]
- Danusevičius D., and Lindgren D., 2004. Progeny testing proceeded by phenotypic pre-selection-timing considerations. Silvae Genet. 53: 20–26. [Google Scholar]
- Falconer D.S. and Mackay T.F.C., 1996. Introduction to quantitative genetics, Longman, Essex, UK, 480 p. [Google Scholar]
- Hannrup B., Jansson G., and Danell Ö., 2007. Comparing gain and optimum test size from progeny testing and phenotypic selection in Pinus sylvestris. Can. J. For. Res. 37: 1227–1235. [CrossRef] [Google Scholar]
- Jansson G., Li B., and Hannrup B., 2003. Time trends in genetic parameters for height and optimal age for parental selection in Scots pine. For. Science 49: 696–705. [Google Scholar]
- Kerr R.J., Goddard M.E., and Jarvis S.F., 1998. Maximising genetic response in tree breeding with constraints on group coancestry. Silvae Genet. 47: 165–173. [Google Scholar]
- Lambeth C.C., 1980. Juvenile-mature correlation in Pinaceae and implications for early selection. For. Sci. 26: 571–580. [Google Scholar]
- Lindgren D., 2005. Unbalances in tree breeding. In: Fedorkov A. (Ed.), Proc. Meeting Nordic Forest Tree Breeders and Forest Geneticists “Status, monitoring and targets for breeding programs”, Syktyvkar, Russia, pp. 45–56. [Google Scholar]
- Lindgren D., and Mullin T.J., 1997. Balancing gain and relatedness in selection. Silvae Genet. 46: 124–129. [Google Scholar]
- Lindgren D., Wei R.-P., and Lee S., 1997. How to calculate optimum family number when starting a breeding program. For. Sci. 43: 206–212. [Google Scholar]
- Lindgren D., Danusevicius D., and Rosvall O., 2008. Balanced forest tree improvement can be enhanced by selecting among many parents but maintaining balance among grandparent. Can. J. For. Res. 38: 2797–2803. [CrossRef] [Google Scholar]
- Lstibùrek M., Mullin T., Lindgren D., and Rosvall O., 2004a. Open-nucleus breeding strategies compared to population-wide positive assortative mating. I. Equal distribution of testing effort. TAG 109: 1196–1203. [Google Scholar]
- Lstibùrek M., Mullin T., Lindgren D., and Rosvall O., 2004b. Open-nucleus breeding strategies compared to population-wide positive assortative mating. II. Unequal distribution of testing effort. TAG 109: 1169–1177. [Google Scholar]
- Rosvall O., 1999. Enhancing gain from long-term forest tree breeding while conserving genetic diversity. Ph.D. thesis, Swedish University of Agricultural Sciences, Umeå, Sweden, 65 p. [Google Scholar]
- Rosvall O., Jansson G., Andersson B., Ericsson T., Karlsson B., Sonesson J., and Stener L.-G., 2001. Genetiska vinster i nuvarande och framtida fröplantager och klonblandningar. (Genetic gain from present and future seed orchards and clone mixes) (in Swedish with English summary). SkogForsk Redogörelse Nr. 1, 41 p. [Google Scholar]
- Ruotsalainen S., 2002. Managing breeding stock in the initiation of a long-term tree breeding program. Ph.D. thesis, Finnish Forest Research Institute, Research Papers 875, 95 p. [Google Scholar]
- Sanchez L.R., 2000. Balanced vs. slightly unbalanced selection. Heredity 84: 685–691. [CrossRef] [PubMed] [Google Scholar]
- Wei R.-P., 1995. Predicting genetic diversity and optimising selection. Ph.D. thesis, Swedish University of Agricultural Sciences, Umeå, Sweden, 64 p. [Google Scholar]
- Wei R.-P., and Lindgren D., 2001. Optimum breeding generation interval considering build-up of relatedness. Can. J. For. Res 31: 722–729. [CrossRef] [Google Scholar]
All Tables
Parameter values for the main scenario A and the alternative scenarios. Scenario B values were the same as for scenario A except that the number of parents per grandparent was 3 and annual budget per grandparent was 20.
Scenario A. Considerations of number of parents per grandparent (PGP). This table is for variants of the main scenario where annual cost per grandparent is 50 and PGP is variable. PF is the proportion of plants selected as parents for the breeding population.
Scenario B. Considerations of parents per grandparent (PGP). Here the gain is given in percentage of that maximizing gain per year for different deviations from the optimal testing. “n.p.”means “value not possible”. PF is the proportion of plants selected as parents for the breeding population.
Testing time considerations. The testing time of 15 y was chosen for the main scenario. Here the annual group merit at some testing times is presented as percentage of the test time maximizing group merit per year for different deviations from the optimal testing. Annual gain and annual group merit are identical unless group coancestry gets a weight, which it does not in the main scenario. While testing an alterative parameter value, the other values are kept at the main scenario values (number of parents per grandparent is 6 (12 per family with SPM)).
All Figures
 |
Figure 1 Two balanced breeding strategies are compared. A sub-line initiated by four founders is shown. The connected lines show the pairs mated. To the left “parent-balance”strategy with within-family selection only, where two families are created and after testing the two best individuals in each are mated. To the right “grandparent-balance”strategy with both within- and among-family selection, where four but smaller families are created and after testing the best two individuals in each of the two best families are mated. |
| In the text | |
 |
Figure 2 Optimal number of parents per grandparent as a function of annual budget (a). Annual gain as a function of the number of parents per grandparent (b). Three curves are shown for different costs per parent (Cparent = 50 for main scenario). Optimum number of parents per grandparent for the main scenario annual budget (50) are indicated by dots on the curves. |
| In the text | |


