EDP Sciences logo
Search
Menu
All issues Volume 67 / No 8 (December 2010) Ann. For. Sci., 67 8 (2010) 815 Full HTML
Free Access
Issue
Ann. For. Sci.
Volume 67, Number 8, December 2010
Article Number 815
Number of page(s) 7
Section Original articles
DOI https://doi.org/10.1051/forest/2010054
Published online 28 October 2010

© INRA, EDP Sciences, 2010

1. Introduction

The xylophone is a percussion instrument made of vibrating wooden bars mounted horizontally and supported by a soft material at the two nodal points of its lowest eigenfrequency (Wegst, 2008). More information on the physical phenomena which governs the motion of waves in elastic bars can be found in many previous works (Brémaud, 2006; Bucur, 2006).

The xylophone is a member of the idiophone group, which is very frequent in African traditional or popular music. Its sound percussion quality is due to the resonance properties of the wood used for its manufacture, which in turn are closely related to its intrinsic properties such as ultrastructure properties, anatomical structure or extractive content (Brancheriau et al., 2006b; Brémaud, 2006; Bucur, 2006; Matsunaga et al., 1999; Norimoto et al., 1986; Obataya, 2000). When a free wooden bar is subjected to an impact, it vibrates at frequencies known as eigenfrequencies. Following the impact, several wave types are likely to be propagated: mainly transversal, torsional and longitudinal waves (Bucur, 2006). However, the sound produced is primarily due to the transversal waves, whose frequencies modes are governed by the geometry and the intrinsic properties of the wooden bar, but also by the imposed boundary conditions (Brancheriau, 2006; Brancheriau et al. 2006b; 2006c; Brémaud, 2006). The resulting vibration damping, materialized by the progressive decrease in vibration amplitude, is caused by the energy dissipation related to environmental conditions (sound radiations) and by the intrinsic properties of the material (energy loss mainly by internal friction of vibrating particles) (Bordonné, 1989; Brancheriau, 2002; Brémaud, 2006; Dunlop and Shaw, 1991).

The main mechanical properties selected by Brancheriau (2006) and Brémaud (2006) to describe the acoustic behavior of wood for xylophone are the specific dynamic modulus (EL/ρ) and the damping coefficient or internal friction (tan δ). Several species are currently indexed and evaluated for the manufacture of xylophones (Brémaud, 2006). According to Bork (1985) and Holz (1996), the wood species generally used for the xylophone manufacture have a high density (ρ) of approximately 0.80 g/cm3 to 0.95 g/cm3, a high dynamic modulus (EL) of circa 15 to 20 GPa, a high degree of hardness and durability and a low tendency to split and crack. They present a low damping coefficient (tan δ), along with low sensitivity to moisture content variations (Brémaud, 2006; Richter, 1988).

Other features such as, the sound radiation coefficient (SRC) and the peak response (PR) are also important parameters to take into account for the acoustic quality of xylophones (Barlow, 1997; Wegst, 2006; 2008). The SRC describes how fast the vibration of a body is damped due to sound radiation (Wegst, 2006). The PR coefficient is directly linked to the magnitude of the vibratory response (Barlow, 1997). According to Wegst (2006; 2009), a high density associated with a high dynamic modulus, a large sound radiation coefficient, a high peak response and a low damping coefficient of the material is particularly desirable in the case of xylophones if one wish to produce a loud sound.

In Mali, the vène is an indigenous species from the Soudanian and Guinean climate areas that is higly appreciated for the manufacture of xylophones. This wood species, dense and rich in extractives (Brémaud, 2006), presenting a distinct ring width (Mariaux, 1967), remains the main source of wood for the manufacture of xylophone instruments in Mali. As regards the ring width, one can emphasize that in certain African climate regions such as the Soudanian and Guinean, two different seasons characterizes the year: a raining season favorable to the tree growth and a dry season which stops the cambial activity in certain species. This phenomenon was already observed by Mariaux (1967) in Pterocarpus erinaceus; it is then possible to consider the visible ring width in this species as natural annual ring width. There is, however, only a limited corpus of scientific research on vène wood. In spite of numerous studies of the acoustic properties of wood, very few published studies are available for Pterocarpus species in general and for Pterocarpus erinaceus in particular. To our knowledge, there have been no other studies concerning the variability of its acoustic quality. According to certain Malian xylophone makers, for selecting the wooden xylophone bars for a best sound quality, the internal part of the tree has to be avoided. The goal of this study was to investigate the acoustic properties of vène wood: (1) along the tree’s radial direction (2) related to geographic origin and (3) to investigate the effect of ring width, basic density and extractive content on these acoustic characteristics. For this purpose, dynamic and specific modulus of elasticity, damping coefficient, sound radiation coefficient, peak response, basic density, extractive content and ring width were assessed to evaluate the wood’s acoustic quality for making xylophone/musical instruments.

2. Materials and methods

2.1. Material selection and preparation

Wood samples were harvested from the natural forests of the Guinean and Soudanian climatic areas of Mali. The Guinean area, located in the extreme southern part of the country, is characterized by average annual precipitations of between 1100 and 1500 mm. Average annual temperature ranges from 26 to 28 °C and the soils are primarily ferrallitic. As for the Soudanian area, it is subjected to a subhumid to semi-arid climate, where rainfall varies from 600 to 1100 mm. The soils, generally of ferruginous type, are relatively deep, sandy and clayey, but of low fertility (Coulibaly, 2003; Nasi and Sabatier, 1988a; 1988b). A total of 5 trees from each area, free from any defect or external deterioration and having reached exploitation age (diameter at breast height ranging from 50 to 60 cm), were cut at 0.5 m above the ground. A 1.50 m long log was cut from each tree. These logs were quarter-sawn into 40 mm thick boards, the central board containing the pith. Boards were selected to avoid the presence of major defects. Failing precise juvenile-mature wood delimitation, it was decided to arbitrarily delimit three radial areas counted from the pith: the internal heartwood (IHW); the median heartwood (MHW) and the external heartwood (EHW). Only the heartwood was subjected to acoustic analyses as the sapwood part was not large enough to allow a correct sampling. After natural drying of the boards, samples with dimensions 360 (L)  ×  15 (R)  ×  30 mm3 (T) were prepared from pith to heartwood-sapwood border and indexed according to geographic origin and radial intra-tree location (IHW, MHW and EHW). Thus a total of 64 clear samples were obtained and conditioned as follows: relative humidity 65 ± 5% and temperature 20 ± 2°C, for 4 weeks in order to equilibrate the moisture content at 12%.

2.2. Acoustic properties

A test method of free-free flexural vibration was used (BING device, http://www.xylo-metry.org/en/softwares.html, Fig. 1). The wood sample was placed on two elastic supports. A vibration was induced by tapping vertically on the sample end with a mallet (a metal stem covered at one end with a hard gum). A microphone was placed at the other end of the specimen to collect the acoustic pressure radiated from the impact. The acoustic signal was then amplified, filtered and sampled (Fig. 1).

The concept of additive synthesis, described by Ystad (1998), was applied to extract the parameters from acoustic sounds. Each temporal signal s(t) can be considered as the sum of exponentially damped sinusoids (Eq. (1)): 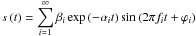(1)where s is the radiated signal over time t, βi the temporal amplitude coefficient, αi the temporal damping, fi is the resonance frequency of order i, and φi is the phase shift. The first resonance oscillations were extracted to determine the first frequency mode f1 and the temporal damping α1. Only the first frequency mode was considered because of its high energy (all modes can be analyzed simultaneously by this device).

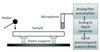thumbnail Figure 1

Acoustic analysis device (BING).

The first vibration frequency f1 is governed, in particular, by the specific dynamic modulus according to the following equation (Eq. (2)) 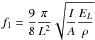(2)where L is the sample length, I is the moment of inertia, A is the sample cross-sectional area and ρ is the density. Equation (2) leads to assess the specific dynamic modulus (EL/ρ) and the dynamic modulus (EL). To calculate the density ρ of each sample, the sample mass was determined using a balance with a resolution of  ± 0.01 g (Mettler PM2000) and the sample dimensions were measured with a precision of  ± 0.02 mm using a slide caliper (Mitutoyo DIGIMATIC ABSOLUTE).

The damping coefficient (tan δ) was calculated based on the sound signal “descriptor” parameters (Brancheriau et al., 2006a) in agreement with the complex modulus concept (Ouis, 2002) applied to the case of transverse vibrations (Brancheriau, 2002) by the following relation (Eq. (3)): 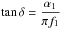(3)where, α1 is the temporal damping associated with f1.

The peak response (PR) is defined as the ratio of the sound radiation coefficient (SRC) to the damping coefficient (tan δ) (Barlow, 1997; Wegst, 2006; Wegst, 2008) in Equation 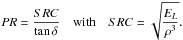(4): (4)

2.3. Ring width

The ring width provides information about the time required by a tree to reach exploitation diameter (Detienne et al., 1989). It visually materializes the influence of growth conditions on the wood. The mean ring width value for each sample was defined as the ratio of the length of a radial segment to the total number of rings counted in this segment. In order to clearly reveal the ring limits, the cross section of each sample bar was subjected to sanding with gradually finer grains (120, 240, 320, 600 and 1200). Thereafter, a binocular magnifier, connected to a camera and a computer, was used to count and to measure the ring width. A small graduated ruler placed on the cross section allowed accurate measurement of ring widths on the PC screen.

2.4. Basic density

It is important to consider the basic density (oven-dry mass over green volume) instead of the density, as it represents an absolute determination of the lignocellulosic matter present in a unit volume of wood (contrary to density which varies according to moisture content). After determination of the acoustic quality descriptors and ring width, three 15 mm sample cubes were cut from three different points of each test-sample (both ends and center) in order to determine the average basic density for each test-sample. These sample cubes were fully saturated using a vacuum-pressure process and ice-cold water in order to limit the dissolution of extractives. Basic density was determined according to the technique recommended by international standard ISO 3129, based on the following relationship (Eq. (5)). 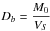(5)where, M0 is the oven dry mass (kg) and Vs is the volume of the cube at saturated state (m3).

2.5. Extractive content

After measuring basic density, most of the remaining test-sample was then reduced to fine 40 mesh (425 microns) sawdust according to ASTM D1105 (1996). The sawdust of several specimens within the same area was mixed in order to obtain enough powder for each determination of extractive content (IHW, MHW and EHW). The total extractive content of wood samples was determined according to ASTM D1105 (1996) by sequential extraction of the sawdust: (1) with ethanol-toluene (1000 mL of ethanol, 427 mL of toluene) during 6 h; (2) with ethanol 95% during 4 h; and (3) with hot water during 3 h.

Table I

Mean value and standard deviation (STD) in brackets for measured properties.

Table II

ANOVA tests for measured properties according to origin and radial-location (NS: not significant at 5% level).

2.6. Statistical analysis

The experimental design for the present study was deemed to be a split plot design, with the origin effect considered as the main plot treatment and location within the tree considered as the sub-plot treatment. All data were subjected to analysis of variance tests (ANOVA test at 95% probability level) using the SPSS 13.0 software package to determine how these characteristics differ according to origin and intra-tree location. Pearson Correlations were used to analyze the degree to which the measured properties are interrelated.

Table III

Pearson correlation coefficients (NS: not significant at 5% level).

thumbnail Figure 2

Fourier transform magnitude (first frequency at 500 Hz).

thumbnail Figure 3

Analytical signal associated with the first frequency (oscillations of the first mode obtained by signal processing).

3. Results and discussions

3.1. Acoustic properties

The results show that the EL,EL/ρ, tanδ and PR values differ significantly according to origin and intra-tree location (Tabs. I and II). The wood samples from the Guinean area possess a higher acoustic quality for the xylophone instrument manufacture than those from the Soudanian area. Indeed, the dynamic modulus (EL), the dynamic specific modulus (EL/ρ) and the peak response (PR) were determined to be significantly higher for wood from the Guinean area than from the Soudanian area. Regardless of origin, significantly higher dynamic modulus (EL), dynamic specific modulus (EL/ρ) and peak response (PR) were determined for wood samples from external and median heartwood (EHW and MHW) than from internal heartwood (IHW). The damping coefficient (tan δ) was found lower for wood from the Guinean area than for wood from the Soudanian area and also significantly lower in EHW and MHW than in IWH (Tab. I). These results could probably explain why the Malian xylophone makers empirically use only the wood from EHW and MHW. The specimens from the two different locations and from the three radial locations show no difference of sound radiation coefficient (SRC, Tab. II). However, one can notice an increase in SRC values from IHW to EHW and higher values for wood from Guinean area than for wood from Soudanian area (Tab. I).

The differences in extractives content, basic density and dynamic modulus values (Tab. I) detected between the different origins and radial intra-tree locations could explain the variability of acoustic properties. The dynamic modulus is well-known to be considerably affected by cell wall properties such as microfibril angle of the S2 layer which usually declines with cambial age and is known to be the main relevant parameter for assessing wood quality (Treacy et al., 2000; Walker and Butterfield, 1996; Zobel and Buijtenen, 1989). The results obtained confirm previous works postulating that a high dynamic modulus and a high density are desirable for xylophone bars (Bork, 1985; Holz, 1996; Wegst, 2006; 2008). Despite a lack of correlation between ring width (RW) and acoustic properties (Tab. III), it is shown that basic density (Db) and acoustic properties increase with a decrease in RW for vène wood from the two studied regions (Tab. I). However, other authors (Kubojima et al., 1997) did not find clear direct relationships between RW and vibrational properties of Spruce wood.

Table III shows that EL/ρ, tanδ and PR are significantly correlated with Db and EC. It was reported that some extractives contribute to improving acoustic properties (Brémaud, 2006; Matsunaga et al., 1999). Furthermore, the damping coefficient (tan δ) decreased with an increase in dynamic specific modulus (EL/ρ) within this Pterocarpus species (Fig. 4). Similar correlations have been reported for different wood species by several researchers (Brémaud, 2006; Norimoto et al., 1986; Obataya et al., 2000; Ono and Norimoto, 1985).

thumbnail Figure 4

Dynamic specific modulus vs. damping coefficient tanδ.

thumbnail Figure 5

Ring widths of vène wood.

3.2. Ring width

The results show that the ring width differs significantly according to origin and radial intra-tree location (Tabs. I, II and Fig. 5). The ring width is significantly higher for wood from the Guinean area than for wood from the Soudanian area. Regardless of geographical origin, the ring width values were found to be significantly higher for samples from IHW than from EHW and MHW of vène wood. The difference in ring width according to the geographical origin could be explained by genetic origin and growth conditions, such as soil quality or water availability (Leclercq, 1979; 1982). The decrease in ring width, from pith to bark, is certainly due to the competition between trees occurring when the vegetation become denser and by changes in initial cambial cells with cambial age (Nepveu, 1994). Similar results were found by Détienne et al. (1989) and Durrieu De Madron et al. (2000).

3.3. Basic density

The basic density is significantly higher for wood from the Guinean area than from the Soudanian area and higher, regardless of origin, for wood from EHW and MHW than from IHW (Tabs. I, II). The variations in basic density of vène wood, according to geographic origin, could be mainly explained by differences in extractive content and growth characteristics such as earlywood and latewood percentage or vessel density within the ring due to differences in the growth conditions of two climatic regions (Leclercq, 1979; 1982). Intra-tree (radial) variation, however, could be directly related to cell wall thickness and to the general trend in extractives distribution in the radial direction (Gominho, 2001; Nepveu, 1994). The probable difference in genetic origin could also explain the difference in basic density between the two geographic origins, i.e. vessel diameter and vessel density.

3.4. Extractive content

The extractive content differs significantly according to origin and intra-tree location (Tabs. I, II). The average extractive content values determined for wood from the Guinean area were significantly higher than for wood from the Soudanian area. Regardless of wood sample geographic origin, the extractive content was determined to be significantly higher in EHW and MHW than in IHW. The difference in extractive content according to geographic origin could be explained by the growth conditions of two climatic areas, such as soil quality or water availability.

4. Conclusion

The main acoustic properties of vène wood were determined using a test method of free-free flexural vibration (BING device): dynamic modulus (EL), specific dynamic modulus (EL/ρ), damping coefficient or internal friction (tan δ), sound radiation coefficient (SRC) and peak response (PR). In addition to these properties, ring width (RW), basic density (Db) and extractive content (EC) were also determined. Samples from two geographic origins (Guinean and Soudanian areas) and three radial intra-tree location (internal: IHW, median: MHW, external: EHW) were tested. The results of this research lead to the following conclusions:

  • EL, EL/ρ and PR were significantly higher for wood from the Guinean area than from the Soudanian area and also higher for EHW and MHW than for IHW. tanδ follows inverse trends.

  • High correlations were shown between tanδ with EL/ρ and tanδ with EC. tanδ decrease with increasing EL/ρ or EC.

  • No significant difference of SRC was found between the two geographic areas and the three radial locations. However, SRC increase from IHW to EHW and were higher for Guinean area than for Soudanian area.

  • Despite no correlation between RW and acoustic properties, it was observed that Db and the acoustic properties increase with a decrease in RW from the two studied regions (except tanδ which follows the inverse trend).

Acknowledgments

This work was supported by “Le Projet franco-malien d’appui à l’enseignement supérieur au Mali” and partially financed by the AgroParisTech /INRA and by an NSERC grant awarded to Stevanovic Tatjana (CRB). The authors would also like to acknowledge Mr Traoré Fatogoma and Traoré N’ge (joiner and xylophone maker/Dionina/Mali) for their help in sampling.

References

  • ASTM 1996. Standard Test Method for preparation of extractives-free wood, ASTM D 1105–1196. [Google Scholar]
  • Barlow C.Y., 1997. Materials selection for musical instruments, In: Proceedings of the Institute of Acoustics, vol. 19, pp. 69–78. [Google Scholar]
  • Bordonné P.A., 1989. Module dynamique et frottement interieur dans le bois, mesures sur poutres flottantes en vibrations naturelles. Ph.D. thesis, Institut National Polytechnique de Lorraine, 109 p. [Google Scholar]
  • Bork I. and Meyer J., 1985. On the tonal evaluation of xylophones. Physikalisch- Technische Bundesanstall Braunschweig, Germany. [Google Scholar]
  • Brancheriau L., 2002. Expertise mécanique des sciages par analyses des vibrations dans le domaine acoustique. Ph.D. thesis, Université de la Méditerranée-Aix-Marseille II, Marseille, 267 p. [Google Scholar]
  • Brancheriau L., 2006. Influence of cross section dimensions on Timoshenko’s shear factor – Application to wooden beams in free-free flexural vibration. Ann. For. Sci. 63: 319–321. [CrossRef] [EDP Sciences] [Google Scholar]
  • Brancheriau L., Baillères H., Détienne P., Kronland R., and Gril J., 2006a. Key signal and wood anatomy parameters related to the acoustic quality of wood for xylophone-type percussion instruments. J. Wood Sci. 52: 270–273. [CrossRef] [Google Scholar]
  • Brancheriau L., Baillères H., Détienne P., Kronland R., and Metzger B., 2006b. Classifying xylophone bar materials by perceptual, signal processing and wood anatomcal analysis. Ann. For. Sci. 63: 73–81. [CrossRef] [EDP Sciences] [Google Scholar]
  • Brancheriau L., Baillères H., and Sales C., 2006c. Acoustic resonance of xylophone bars: experimental and analytic approaches of frequency shift phenomenon during the tuning operation of xylophone bars. Wood Sci. Technol. 40: 94–106. [CrossRef] [Google Scholar]
  • Brémaud I., 2006. Diversité des bois utilisés ou utilisables en facture d’instruments de musique. Ph.D. thesis, Université Montpellier II, Montpellier, 295 p. [Google Scholar]
  • Bucur V., 2006. Acoustics of wood, 2nd edition, Springer, 393 p. [Google Scholar]
  • Coulibaly A., 2003. Profiles of forage ressource: Mali, Food and Agriculture Organization of the United Nations, http://www.fao.org/. [Google Scholar]
  • Détienne P., Oyono F., Durrieu de Madron L., Demarquez B., and Nasi R., 1998. L’analyse de cernes: applications aux études croissance de quelques essences en peuplement naturels de forêt dense africaine, Montpellier, CIRAD-Forêt. [Google Scholar]
  • Dunlop J. and Shaw M., 1991. Acoustic properties of some Australian woods. Catgut Acoust. Soc. J. 1: 17–20. [Google Scholar]
  • Durrieu De Madron L., Nasi R., and Détienne P., 2000. Accroissements diamétriques de quelques essences en forêt dense africaine. Bois For. Trop. 263: 63–74. [Google Scholar]
  • Gominho J., Figueira J., Rodrigues J.C., and Pereira H., 2001. Within-tree variation of heartwood, extractives and wood density in the eucalypt hybrid urograndis (Eucalyptus grandis × E. urophylla). Wood and Fiber Sci. 33: 3–8. [Google Scholar]
  • Holz D., 1996. Acoustically important properties of xylophone-bar materials: can tropical woods be replaced by European species? Acta Acustica 82: 878–884. [Google Scholar]
  • ISO 3129, 1975. Bois-Méthodes d’échantillonnage et conditions générales pour les essais physiques et mécaniques, 4 p. [Google Scholar]
  • Kubojima Y., Okano T., and Ohta M., 1997. Effect of annual ring widths on structural and vibrational properties of wood. Mokuzai Gakkaishi. 43: 634–641. [Google Scholar]
  • Leclercq A., 1979. Influence du milieu sur les propriétés physico-mécaniques du bois de hêtre (Fagus silvatica). Bull. Rech. Agron. Gembloux 14: 213–240. [Google Scholar]
  • Leclercq A., 1982. Influence du milieu sur la structure anatomique du bois de hêtre (Fagus silvatica L). Bull. Rech. Agron. Gembloux 17: 363–376. [Google Scholar]
  • Mariaux A., 1967. Les cernes dans les bois tropicaux africains, nature et périodicité. Bois For. Trop. 113: 3–14. [Google Scholar]
  • Matsunaga M., Minato K., and Nakatsubo F., 1999. Vibrational properties changes of spruce wood by impregnation with water soluble extractives of pernambuco (Guilandina echinata Spreng.). J. Wood Sci. 45: 470–474. [CrossRef] [Google Scholar]
  • Nasi R. and Sabatier M., 1988a. Inventaire des ressources ligneuses au Mali. Rapport de synthèse, première phase, Les formations végétales. Ministère chargé des Ressources Naturelles et de l’Élevage, Direction Nationale des Eaux et Forêts, BDPA/SCET-AGRI, CTFT (CIRAD), 205 p. [Google Scholar]
  • Nasi R. and Sabatier M,. 1988b. Inventaire des ressources ligneuses au Mali. Rapport technique, première phase, Inventaire des formations végétales, Ministère chargé des Ressources Naturelles et de l’Élevage, Direction Nationale des Eaux et Forêts, BDPA/SCETAGRI, CTFT (CIRAD), 115 p. [Google Scholar]
  • Nepveu G., 1994. Le bois matériau d’ingénierie – Variabilité, ARBOLOR, Nancy, pp. 126–182. [Google Scholar]
  • Norimoto M., Tanaka F., Ohogama T., and Ikimune R., 1986. Specific dynamic Young’s modulus and internal friction of wood in the longitudinal direction. Wood Res. Tech. Notes. 22: 53–65. [Google Scholar]
  • Obataya E., Ono T., and Norimoto M., 2000. Vibrational properties of wood along the grain. J. Mater. Sci. 35: 2993–3001. [CrossRef] [Google Scholar]
  • Ono T. and Norimoto M., 1985. Anisotropy of dynamic yong’s modulus and internal friction in wood. Jpn. J. Appl. Phys. 24: 960–964. [CrossRef] [Google Scholar]
  • Ouis D., 2002. On the frequency dependence of the modulus of elasticity of wood. Wood Sci. Technol. 36: 335–346. [CrossRef] [Google Scholar]
  • Richter H.G., 1988. Holz als Rohstoff für den Musikinstrumentenbau, Moeck Verlag, Celle, 44 p. [Google Scholar]
  • Treacy M., Evertsen J., and Dhubháin A., 2000. A comparison of mechanical and physical wood properties of a range of Sitka spruce provenances, COFORD – National Council for Forest Research and Development, Ireland, 35 p. [Google Scholar]
  • Ystad S., 1998. Sound modeling using a combination of physical and signal models. Ph.D. thesis, Université de la Méditerranée-Aix-Marseille II, Marseille, 130 p. [Google Scholar]
  • Walker J.C.F. and Butterfield B.G., 1996,. The importance of the microfibril angle for the processing industries, New Zealand Forestry, pp. 34–40. [Google Scholar]
  • Wegst U.G.K., 2006. Wood for Sound. Am. J. Bot. 93: 1439–1448. [CrossRef] [PubMed] [Google Scholar]
  • Wegst U.G.K., 2008. Bamboo and Wood in Musical Instruments. Ann. Rev. Mat. Res. 38: 323–349. [CrossRef] [Google Scholar]
  • Zobel B.J., and Van Buijtenen J.P., 1989. Wood variation, its causes and control, Springer, 363 p. [Google Scholar]

All Tables

Table I

Mean value and standard deviation (STD) in brackets for measured properties.

In the text
Table II

ANOVA tests for measured properties according to origin and radial-location (NS: not significant at 5% level).

In the text
Table III

Pearson correlation coefficients (NS: not significant at 5% level).

In the text

All Figures

thumbnail Figure 1

Acoustic analysis device (BING).
In the text
thumbnail Figure 2

Fourier transform magnitude (first frequency at 500 Hz).
In the text
thumbnail Figure 3

Analytical signal associated with the first frequency (oscillations of the first mode obtained by signal processing).
In the text
thumbnail Figure 4

Dynamic specific modulus vs. damping coefficient tanδ.
In the text
thumbnail Figure 5

Ring widths of vène wood.
In the text